Todos los vídeos de Draw Curiosity están subtitulados en español e inglés. Este blog extiende los conceptos presentados en el vídeo.
El 22 de julio es el Día de Aproximación de Pi, al igual que mi cumpleaños – o ‘cumpileaños’! Mientras que yo celebraba mi vigésimo tercera rotación alrededor del sol, el resto del mundo podía celebrar la perfecta combinación de un mes y día que representan de manera más precisa el valor de pi, duplicando el número de días del año en el cual es aceptable disfrutar de pasteles redondos para disfrutar de un número tan redondo.
Un breve recordatorio, pi ó π es una constante matemática, un número irracional que representa la razón entre el diámetro de una circunferencia y su perímetro. Si el diámetro de una circunferencia es 1, su perímetro es equivalente a π.
¿Qué Métodos Empleaban los Matemáticos para Aproximar Pi?
Tras publicar este vídeo, algunos de mis suscriptores me dijeron que les habría gustado una explicación más profunda acerca de los métodos empleados para aproximar pi – algo que reconozco me hubiera gustado compartir en mi vídeo también. Sin embargo, las «Analytics» de YouTube son bastante detalladas, y me demuestran que la gente suele quitar el vídeo en cuanto aparece una ecuación, y esa es la razón por la cual me decanté por la Historia de Pi, algo más digerible. Sin embargo, me encanta que compartáis ese entusiasmo de querer saber más de pi conmigo, ya que seguramente emplee futuros días de Pi y de Aproximación de Pi para contároslo con más detalles – y no os voy a mentir, yo creo que las ecuaciones molan!
Así que, aquí va un resumen de los dos métodos principales empleados para estimar el valor real de pi:
Aproximaciones Diofánticas
Las primeras aproximaciones de pi, como aquellos empleados por los egipcios, Arquímedes y Liu Hiu, eran todas aproximaciones diofánticas. En resumen, una aproximación diofántica es la aproximación de un número real empleando números racionales.
Un número real es el conjunto de todos los números racionales e irracionales. Los números racionales se pueden expresar como fracciones, mientras que los irracionales no se pueden. Pi π es un número irracional, lo cual significa que contiene una cantidad infinita y no periódica de cifras decimales, y por tanto su valor real no puede representarse en una fracción. A pesar de ello, Arquímedes y Liu Hiu realizaron muy buenas estimaciones de pi, y ambos emplearon polígonos de muchos lados para aproximar su valor.
Definieron cotas superiores e inferiores mediante la inscripción y circunscripción de polígonos con una gran cantidad de lados, y calculando el perímetro de cada pareja de polígonos. De esta manera, sabían que el valor de π se hallaba entre esos dos valores.

Emplearon polígonos con muchos lados para definir de manera más exacta las cotas superiores e inferiores en el cual se hallaría pi. En el caso de Arquímedes de Siracusa, aproximó el valor de pi a:
el cual es la fracción más precisa con tan sólo 2 dígitos en el numerador. Lo hizo utilizando un polígonos de 96 lados. El valor de 22/7 era su cota superior de un 96-gono circunscrito, mientras que su cota inferior era 223/71, calculado a partir de un 96-gono inscrito.
Liu Hiu llevó la aproximación de pi un paso más allá. Su trabajo mostraba un gran dominio del cálculo, y fue conocido por emplear un algoritmo ligeramente distinto y más rápido que empleaba los áreas de los polígonos en lugar de sus perímetros. Esto se debía a que era consciente de la proporcionalidad establecida entre el área y el perímetro de un polígono, y basado en las herramientas que tenía a mano, calcular el área era un proceso más sencillo. Fue más allá que Arquímedes y estimó el valor de pi usando un polígono de 196 lados:

Muchos matemáticos emplearon métodos similares para estimar pi. De los matemáticos citados en este vídeo, Ludolph van Ceulen habrá sido de los últimos en replicar el método de Arquímedes, empleando un polígono de 262 lados, y extendiendo el número de decimales conocidos de pi a 35. Ludolph estaba tremendamente orgulloso de este logro, y pidió que lo grabasen en su tumba.
Series Infinitas
A partir del siglo XIV, el uso de expansiones infinitas y algoritmos se convirtió gradualmente en el método preferido para aproximar el valor de pi. Madhava de Sangamagrama fue un pionero en este aspecto, ya que fue el primero en proponer una serie infinita para calcular el valor de pi:
Otro logro notable de Madhava es que también se le ocurrió la manera de calcular el error correspondiente en función del número n de términos computados de su serie.
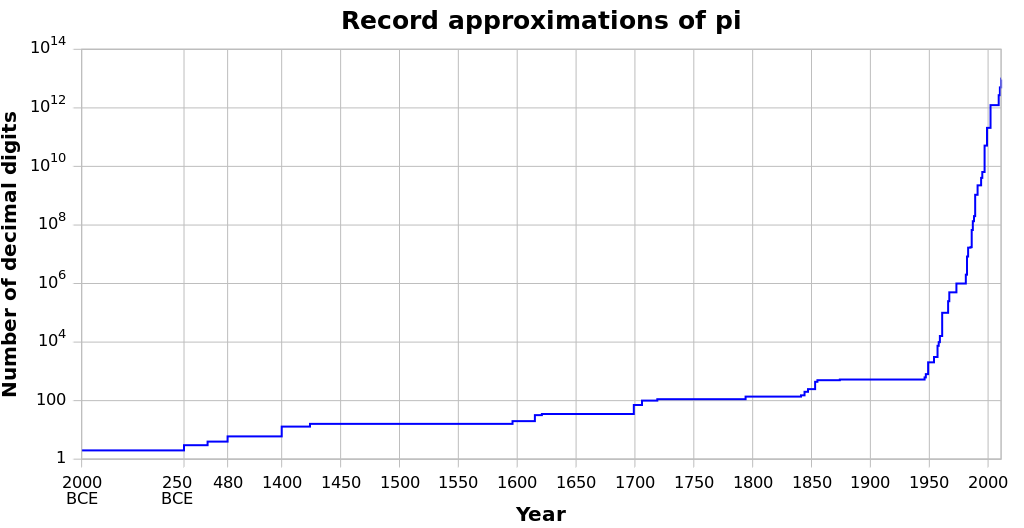
En 1910, Ramanujan ideó un algoritmo que sería adaptado para crear la serie más eficiente para computar pi de manera rápida, y con la introducción de computadoras y superordenadores, el número de decimales de pi conocidas ha aumentado de manera exponencial. La gráfica anterior mostraba el número de decimales conocidos de pi a lo largo del tiempo – y es muy obvio cuando aparatos como calculadoras y ordenadores se inventaron y entraron en la escena. De hecho, a la hora de desarrollar ordenadores, su capacidad de computar décimas de pi se empleaba como un examen para verificar si eran capaces de calcular valores de manera precisa y exacta – y como ya sabemos, mejor estar correctos de manera aproximada, que exactamente incorrectos!
Espero que hayas disfrutado este post y hayas aprendido algo nuevo hoy. Me encantaría saber qué pensáis acerca de este tema, ¡así que sentiros libres de expresaros en los comentarios! Si disfrutaste de este blog y quieres ser notificado de nuevas entradas, puedes suscribirte al mailing list aquí y subscribirte al canal de YouTube!
