All Draw Curiosity videos are fully subtitled in English and Spanish. The blog post builds on the concepts touched upon in the video.
The 22nd of July is Pi Approximation Day, as well as my birthday – or ‘Pirthday’! Whilst I celebrated revolving around the sun approximately 23 times, everyone else could rejoice in a combination of month and day that more accurately represents pi than the official pi day – doubling the days of the year it is acceptable to consume pie to celebrate such a round number.
For a brief reminder, pi or π is a mathematical constant, an irrational number which conveys the ratio between a circumference’s diameter and its perimeter. If a circumference’s diameter is 1, then its perimeter is equal to π.
What Methods Did Mathematicians Use to Approximate Pi?
After publishing the video, several of my viewers said they would have liked a more in-depth explanation on the methods used to approximate pi – something which I admit I would have liked to have shared in my video too. However, YouTube analytics are very insightful and my experience is that people tend to click away when they see an equation, which was why I opted for a more digestible History of Maths this time round. However, it is great to hear this enthusiasm, because it means that I could use future Pi and Pi Approximation Days to explain even more pi-tastic concepts – and I won’t lie, I think equations are pretty cool!
So without further ado, these were the two main approaches used to calculate pi to as many decimal places as possible:
Diophantine Approximations
The early approximations of pi, such as those carried out by the Egyptians, Archimedes and Liu Hiu, were all diophantine approximations. In short, a diophantine approximation is the approximation of a real number using rational numbers.
A real number is the set containing all rational and irrational numbers. Rational numbers can be expressed as fractions, whereas irrational numbers cannot. Pi π is an irrational number, which means it is followed by an infinite quantity of decimal places, and therefore its true value cannot be represented in a fractional manner. Nonetheless, Archimedes and Liu Hiu made very good approximations of pi, and both employed polygons with very large numbers of sides to approximate pi.
They defined the upper and lower bounds by inscribing and circumscribing polygons with increasingly larger number of sides onto a circle, and calculated the perimeter of each pair of polygons. That way, they knew that π was located in between those two values.

They employed polygons with increasingly larger number of sides to define the upper and lower bounds within which pi would be found. In the case of Archimedes of Syracuse, he approximated pi to be:
which is the most accurate fraction with 2 digits in the numerator. He did so using a polygon with 96 sides. The value of 22/7 was his upper limit from a circumscribed 96-gon, whilst his lower limit was 223/71, calculated from an inscribed 96-gon.
Liu Hiu took the estimation of pi a step further. His work displayed a great dominion of calculus, and was known to use a slightly different and faster algorithm which used the areas of polygons rather than their perimeters. This was because he was aware of the proportionality established between them, and calculating the area was a simpler process with the tools he had to hand. He went a lot further than

Archimedes, and estimated the value of pi using a 196-sided polygon:
Plenty of mathematicians also used similar methods to estimate pi. From mathematicians in this video, Ludolph van Ceulen may have been one of the last to replicate Archimedes’ method using a polygon with 262 sides and extended the number of known decimal places to 35. He was incredibly proud of this feat, and asked for it to be engraved on his tombstone.
Infinite Series
From the 14th Century onwards, using infinite expansions and algorithms became a more popular approach to calculating pi. Madhava de Sangamagrama was a pioneer in this respect, for he was the first to come up with a series to calculate pi:
Another remarkable feat of Madhava was that he also came up with a means of calculating an error term corresponding to the number of n terms computed.
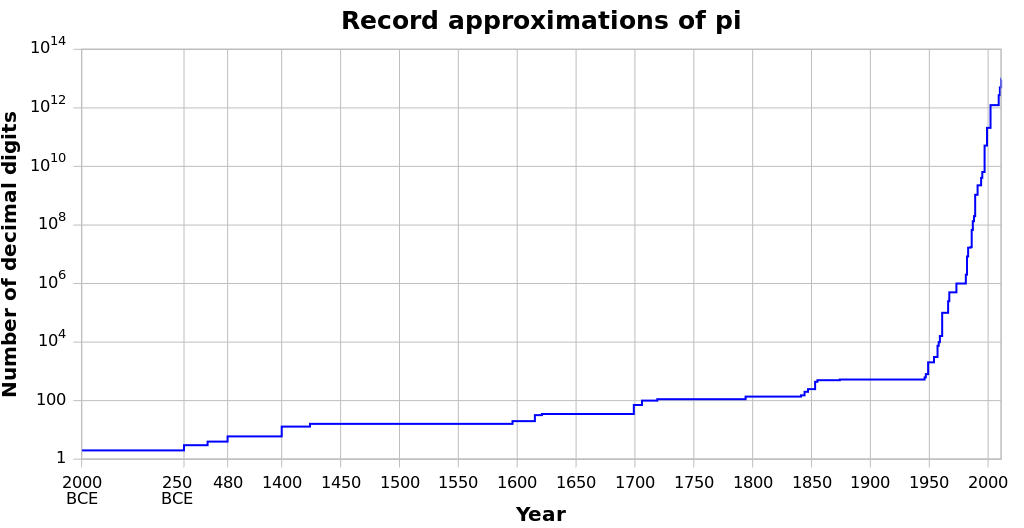
In the 1910s, Ramanujan devised an algorithm which was adapted into the fastest performing series to compute pi, and with the introduction of computers and supercomputers, the number of decimal places of pi known has increased exponentially. The previous graph in fact depicts the number of known decimal places of pi over time – and it becomes very obvious when computational devices such as calculators and computers entered the scene. When developing computers, their ability to compute digits of pi was employed as a test to verify their ability to compute values accurately and precisely – and as we already know, it is best to be approximately right, than exactly wrong!
I hope you enjoyed and learned something new today! Let me know what you think in the comments – I would love to know! If you enjoyed this blog and would like to be notified of new entries, consider signing up to the mailing list here and subscribing to the YouTube channel!
